1. Der Schall
Unter Schall versteht man mechanische Schwingungen in elastischen Medien. Schall kann sich in Flüssigkeiten, Festkörpern und Gasen ausbreiten. Eine Kraft bewegt die Teilchen aus ihrer Ruhelage, um diese die Teilchen dann periodisch schwingen. Die dabei erzeugte Energie wird in Form einer Welle an die benachbarten Mediumteilchen weitergeben. In der akustischen Messtechnik ist dieses Medium meistens Luft. Die Luft transportiert die Energie einer Schallquelle zum Mikrofon oder zum Ohr. Diese Energie wird durch Luftdichteschwankungen, die sich wellenförmig ausbreiten, transportiert.
Die Anzahl der Druckänderungen pro Sekunde nennt man Frequenz(f). Sie wird in Hertz(Hz) gemessen. Die Frequenz des Schalls erzeugt einen charakteristischen Ton. So besitzen tiefe Töne eine niedrige Frequenz und hohe Töne eine hohe Frequenz.
Die Druckänderungen breiten sich mit einer bestimmten Geschwindigkeit(c) in dem Medium aus. Diese Ausbreitungsgeschwindigkeit ist von vier Parametern abhängig, wie aus folgender Formel ersichtlich wird.
c=√((γ R T)/m_Mol
In Luft und bei Raumtemperatur entspricht dies einer Geschwindigkeit von 343 m/s.
Wenn die Geschwindigkeit und die Frequenz bekannt sind, lässt sich daraus die Wellenlänge (λ) berechnen, das ist der Abstand zwei aufeinander folgender Druckspitzen.
λ=c/f
Mit dieser Gleichung lässt sich somit die Wellenlänge verschiedener Frequenzen berechnen. So ergibt sich z.B. bei 16 Hz eine Wellenlänge von 21,5 m und bei 16 kHz nur 2,15 cm. Also sinkt mit zunehmender Frequenz die Wellenlänge des Schalls.
2. Körperschall
Die Analyse von schwingenden Strukturen, wie sie in vielen Teilbereichen des täglichen Lebens auftreten, ist ein wichtiges Gebiet der akustischen Messtechnik. Diese Strukturschwingungen werden auch Körperschall genannt. Neben Longitudinalwellen können in Festkörpern auch Transversalwellen transportiert werden, bei denen eine Schwingung senkrecht zur Ausbreitungsrichtung erfolgt. Diese Wellen breiten sich unabhängig voneinander aus. Die Übertragungsgeschwindigkeit in Festkörpern wird über die Dichte, über das Schubmodul bei Transversalwellen und über das Elastizitätsmodul bei Longitudinalwellen beeinflusst. Durch die Koppelung dieser beiden Wellenarten entstehen weitere Arten von Körperschallwellen. Eine der wichtigsten sind die Biegewellen. Biegewellen rufen eine Bauteilverformung (bei Platten und Stäben) hervor und sind die wesentliche Ursache für die Abstrahlung von Luftschall bei Festkörpern. [1]
3. Luftschall
Schallwellen, die sich über die Luft ausbreiten, werden als Luftschall bezeichnet. Im Gegensatz zum Körperschall besteht Luftschall nur aus Longitudinalwellen, da Gase keine Scherkräfte übertragen können. Schallereignisse in der Luft sind dementsprechend zeitliche und örtliche Schwankungen des statischen Luftdrucks. Luftschall ist der Schall, den das menschliche Ohr wahrnehmen kann und auch der Schall, der in der Akustik gemessen wird.
4. Schallfeldgrößen
Die wichtigsten Schallfeldgrößen bei Schallausbreitung in Luft sind der Schallwechseldruck p und die Schallschnelle .
Der Schallwechseldruck p (Schalldruck) ist dem statischen Druck (Luftdruck) des umgebenden Mediums überlagert,
| p=F/A |
mit einer Kraft F, die auf eine Fläche A wirkt.
Der Gesamtdruck ergibt sich aus der Summe des Schallwechseldrucks mit dem statischen Druck.
Zur Vereinfachung wird in der Praxis anstelle des Schalldrucks häufig der Schalldruckpegel angegeben, da der hörbare Bereich des Schalldrucks acht Zehnerpotenzen umfasst und die Angabe in Pa unübersichtlich wäre:
| L=20 logp/p0 |
Die Angabe des Schalldruckpegels erfolgt in Dezibel. Das Dezibel basiert auf dem logarithmierten Verhältnis einer gemessenen Größe zu einem Bezugspegel. Als Bezugsdruck p0 wird die Hörschwelle von 20 Pa verwendet.
Die Schallschnelle gibt an mit welcher Wechselgeschwindigkeit die Teilchen um ihre Ruhelage schwingen. Die Schallschnelle ist eine vektorielle Größe und berechnet sich als Ableitung der Auslenkung des schwingenden Teilchens nach der Zeit. Sie wird in m/s angegeben.
| ν=dξ/dt [m/s] |
Druck und Schnelle stehen in einer bestimmten Phasenbeziehung zueinander, die je nach Art des Schallfeldes verschieden ist. Bei ebenen fortschreitenden Wellen befinden sich beide Größen in Phase. Bei geschlossenen Rohrenden in einer Rohrleitung bspw. befinden sie sich zu 90° phasenverschoben. Im Vergleich zur Schallgeschwindigkeit ist die Schallschnelle wesentlich kleiner. Bei der Hörschwelle eines 1 kHz-Tones beträgt sie gerade einmal 5*10-8 m/s. [2]
Genau wie der Schalldruck und die Schallschnelle lässt sich auch die Energie im Schallfeld als sich ausbreitende Welle beschreiben, die sich sowohl zeitlich als auch örtlich periodisch ändert. Als Schallintensität bezeichnet man die pro Zeiteinheit durch ein Flächenelement hindurchtretende Schallenergie. Im ebenen Schallfeld ist sie das Produkt aus Schalldruck und Schallschnelle:
|
I=p v=p^2/Zo |
Die Schallleistung ist die Energie, die pro Zeiteinheit durch eine senkrecht zur Ausbreitungsrichtung stehende und beliebig große Fläche A hindurchtritt.
|
P=I A [W] |
Die Schallkennimpedanz Zo ist eine charakteristische Größe des Ausbreitungsmediums. Sie errechnet sich aus dem Produkt des spezifischen Gewichts und der Ausbreitungsgeschwindigkeit c.
|
Zo=ρ c |
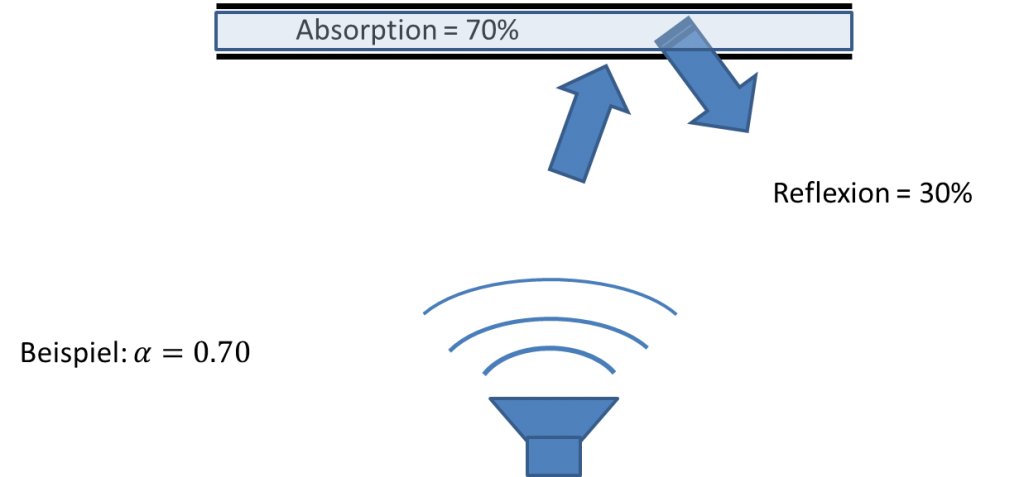
5. Reflexion und Absorption
Trifft eine ebene Schallwelle auf eine unendlich ausgedehnte glatte Wand, so wird sie nach dem Reflexionsgesetz zurückgeworfen. Ebene, schallharte, nicht absorbierende Gegenstände reflektieren den Schall somit gut. Man spricht auch von gerichteter Reflexion. Dabei ist der Reflexionsgrad ein Maß für die reflektierte Intensität, die von außen kommt.
Der Schallabsorptionsgrad gibt an welcher Teil der Leistung einer auftreffenden Welle von einer Fläche absorbiert, d.h. aufgenommen wird. Wenn findet keine Absorption statt und der ganze Schall wird reflektiert. Bei wird der komplette Schall absorbiert.
Für die Schallempfindung in einem Raum spielt das Verhältnis von absorbiertem zu reflektiertem Schall eine ausschlaggebende Rolle. Für Schall ergibt sich der Zusammenhang:
[1] M. Möser, Technische Akustik, 8th ed. Berlin: Springer, 2009.
[2] P. Zeller, Ed., Handbuch Fahrzeugakustik, 1st ed. Viewg+Teubner GWV Fachverlage GmbH, 2009.